Dispelling Maxwell's demon

Maxwell’s demon is one of the most famous thought experiments in the history of physics, a puzzle first posed in the 1860s that continues to shape scientific debates to this day. I’ve struggled to make sense of it for years. Last week I had some time and decided to hunker down and figure it out, and I think I succeeded. The following post describes the fruits of my efforts.
At first sight, the Maxwell’s demon paradox seems odd because it presents a supernatural creature tampering with molecules of gas. But if you pare down the imagery and focus on the technological backdrop of the time of James Clerk Maxwell, who proposed it, a profoundly insightful probe of the second law of thermodynamics comes into view.
The thought experiment asks a simple question: if you had a way to measure and control molecules with perfect precision and at no cost, will you able to make heat flow backwards, as if in an engine?
Picture a box of air divided into two halves by a partition. In the partition is a very small trapdoor. It has a hinge so it can swing open and shut. Now imagine a microscopic valve operator that can detect the speed of each gas molecule as it approaches the trapdoor, decide whether to open or close the door, and actuate the door accordingly.
The operator follows two simple rules: let fast molecules through from left to right and let slow molecules through from right to left. The temperature of a system is nothing but the average kinetic energy of its constituent particles. As the operator operates, over time the right side will heat up and the left side will cool down — thus producing a temperature gradient for free. Where there’s a temperature gradient, it’s possible to run a heat engine. (The internal combustion engine in fossil-fuel vehicles is a common example.)
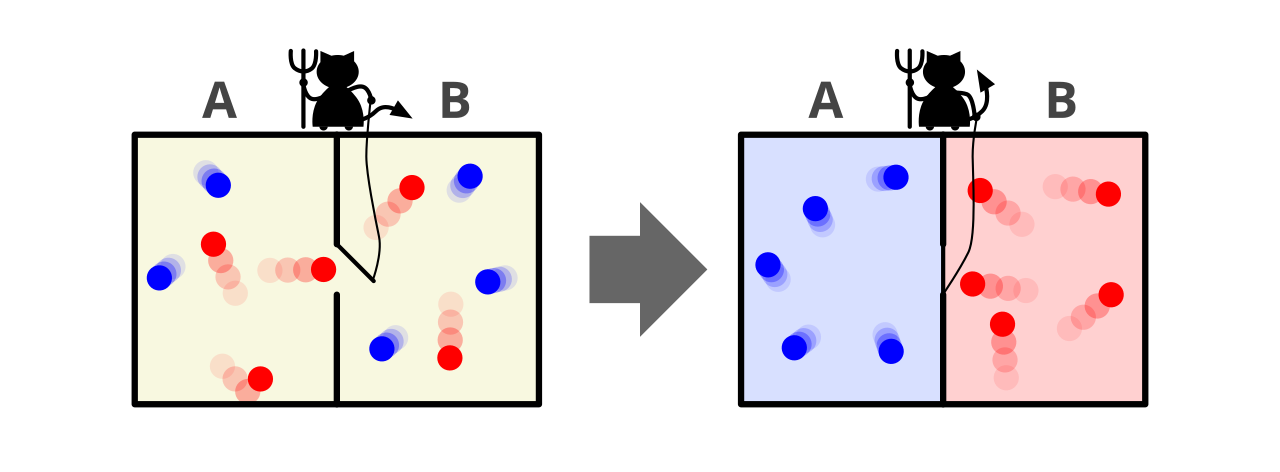
But the possibility that this operator can detect and sort the molecules, thus creating the temperature gradient without consuming some energy of its own, seems to break the second law of thermodynamics. The second law states that the entropy of a closed system increases over time — whereas the operator ensures that the temperature will decrease, violating the law. This was the Maxwell's demon thought experiment, with the demon as a whimsical stand-in for the operator.
The paradox was made compelling by the silent assumption that the act of sorting the molecules could have no cost — i.e. that the imagined operator didn't add energy to the system (the air in the box) but simply allowed molecules that are already in motion to pass one way and not the other. In this sense the operator acted like a valve or a one-way gate. Devices of this kind — including check valves, ratchets, and centrifugal governors — were already familiar in the 19th century. And scientists assumed that if they were scaled down to the molecular level, they'd be able to work without friction and thus separate hot and cold particles without drawing more energy to overcome that friction.
This detail is in fact the fulcrum of the paradox, and the thing that'd kept me all these years from actually understanding what the issue was. Maxwell et al. assumed that it was possible that an entity like this gate could exist: one that, without spending energy to do work (and thus increase entropy), could passively, effortlessly sort the molecules. Overall, the paradox stated that if such a sorting exercise really had no cost, the second law of thermodynamics would be violated.
The second law had been established only a few decades before Maxwell thought up this paradox. If entropy is taken to be a measure of disorder, the second law states that if a system is left to itself, heat will not spontaneously flow from cold to hot and whatever useful energy it holds will inevitably degrade into the random motion of its constituent particles. The second law is the reason why perpetual motion machines are impossible, why the engines in our cars and bikes can’t be 100% efficient, and why time flows in one specific direction (from past to future).
Yet Maxwell's imagined operator seemed to be able to make heat flow backwards, sifting molecules so that order increases spontaneously. For many decades, this possibility challenged what physicists thought they knew about physics. While some brushed it off as a curiosity, others contended that the demon itself must expend some energy to operate the door and that this expense would restore the balance. However, Maxwell had been careful when he conceived the thought experiment: he specified that the trapdoor was small and moved without friction, so it could in principle operate in a negligible way. The real puzzle lay elsewhere.
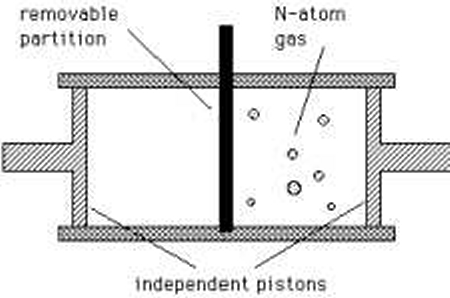
In 1929, the Hungarian physicist Leó Szilard sharpened the problem by boiling it down to a single-particle machine. This so-called Szilard engine imagined one gas molecule in a box with a partition that could be inserted or removed. By observing on which side the molecule lay and then allowing it to push a piston, the operator could apparently extract work from a single particle at uniform temperature. Szilard showed that the key step was not the movement of the piston but the acquisition of information: knowing where the particle was. That is, Szilard reframed the paradox to be not about the molecules being sorted but about an observer making a measurement.
(Aside: Szilard was played by Máté Haumann in the 2023 film Oppenheimer.)
The next clue to cracking the puzzle came in the mid-20th century from the growing field of information theory. In 1961, the German-American physicist Rolf Landauer proposed a principle that connected information and entropy directly. Landauer's principle states that while it's possible in principle to acquire information in a reversible way — i.e. to be able to acquire it as well as lose it — erasing information from a device with memory has a non-zero thermodynamic cost that can't be avoided. That is, the act of resetting a memory register of one bit to a standard state generates a small amount of entropy (proportional to Boltzmann's constant multiplied by the logarithm of two).
The American information theorist Charles H. Bennett later built on Landauer's principle and argued that Maxwell's demon could gather information and act on it — but in order to continue indefinitely, it'd have to erase or overwrite its memory. And that this act of resetting would generate exactly the entropy needed to compensate for the apparent decrease, ultimately preserving the second law of thermodynamics.
Taken together, Maxwell's demon was defeated not by the mechanics of the trapdoor but by the thermodynamic cost of processing information. Specifically, the decrease in entropy as a result of the molecules being sorted by their speed is compensated for by the increase in entropy due to the operator's rewriting or erasure of information about the molecules' speed. Thus a paradox that'd begun as a challenge to thermodynamics ended up enriching it — by showing information could be physical. It also revealed to scientists that entropy is disorder in matter and energy as well as is linked to uncertainty and information.
Over time, Maxwell's demon also became a fount of insight across multiple branches of physics. In classical thermodynamics, for example, entropy came to represent a measure of the probabilities that the system could exist in different combinations of microscopic states. That is, the probabilities referred to the likelihood that a given set of molecules could be arranged in one way instead of another. In statistical mechanics, Maxwell's demon gave scientists a concrete way to think about fluctuations. In any small system, random fluctuations can reduce entropy for some time in a small portion. While the demon seemed to exploit these fluctuations, the laws of probability were found to ensure that on average, entropy would increase. So the demon became a metaphor for how selection based on microscopic knowledge could alter outcomes but also why such selection can't be performed without paying a cost.

For information theorists and computer scientists, the demon was an early symbol of the deep ties between computation and thermodynamics. Landauer's principle showed that erasing information imposes a minimum entropy cost — an insight that matters for how computer hardware should be designed. The principle also influenced debates about reversible computing, where the goal is to design logic gates that don't ever erase information and thus approach zero energy dissipation. In other words, Maxwell's demon foreshadowed modern questions about how energy-efficient computing could really be.
Even beyond physics, the demon has seeped into philosophy, biology, and social thought as a symbol of control and knowledge. In biology, the resemblance between the demon and enzymes that sorts molecules has inspired metaphors about how life maintains order. In economics and social theory, the demon has been used to discuss the limits of surveillance and control. The lesson has been the same in every instance: that information is never free and that the act of using it imposes inescapable energy costs.
I’m particularly taken by the philosophy that animates the paradox. Maxwell's demon was introduced as a way to dramatise the tension between the microscopic reversibility of physical laws and the macroscopic irreversibility encoded in the second law of thermodynamics. I found that a few questions in particular — whether the entropy increase due to the use of information is a matter of an observer's ignorance (i.e. because the observer doesn't know which particular microstate the system occupies at any given moment), whether information has physical significance, and whether the laws of nature really guarantee the irreversibility we observe — have become touchstones in the philosophy of physics.
In the mid-20th century, the Szilard engine became the focus of these debates because it refocused the second law from molecular dynamics to the cost of acquiring information. Later figures such as the French physicist Léon Brillouin and the Hungarian-Canadian physicist Dennis Gabor claimed that it's impossible to measure something without spending energy. Critics however countered that these requirements stipulated the need for specific technologies that would in turn smuggle in some limitations — rather than stipulate the presence of a fundamental principle. That is to say, the debate among philosophers became whether Maxwell's demon was prevented from breaking the second law by deep and hitherto hidden principles or by engineering challenges.
This gridlock was broken when physicists observed that even a demon-free machine must leave some physical trace of its interactions with the molecule. That is, any device that sorts particles will end up in different physical states depending on the outcome, and to complete a thermodynamic cycle those states must be reset. Here, the entropy is not due to the informational content but due to the logical structure of memory. Landauer solidified this with his principle that logically irreversible operations such as erasure carry a minimum thermodynamic cost. Bennett extended this by saying that measurements can be made reversibly but not erasure. The philosophical meaning of both these arguments is that entropy increase isn't just about ignorance but also about parts of information processing being irreversible.

In the quantum domain, the philosophical puzzles became more intense. When an object is measured in quantum mechanics, it isn't just about an observer updating the information they have about the object — the act of measuring also seems to alter the object's quantum states. For example, in the Schrödinger's cat thought experiment, checking whether there's a cat in the box also causes the cat to default to one of two states: dead or alive. Quantum physicists have recreated Maxwell's demon in new ways in order to check whether the second law continues to hold. And over the course of many experiments, they've concluded that indeed it does.
The second law didn't break even when Maxwell's demon could exploit phenomena that aren’t available in the classical domain, including quantum entanglement, superposition, and tunnelling. This was because, among others, quantum mechanics also has some restrictive rules of its own. For one, some physicists have tried to design "quantum demons" that use quantum entanglement between particles to sort them without expending energy. But these experiments have found that as soon as the demon tries to reset its memory and start again, it must erase the record of what happened before. This step destroys the advantage and the entropy cost returns. The overall result is that even a "quantum demon" gains nothing in the long run.
For another, the no-cloning theorem states that you can't make a perfect copy of an unknown quantum state. If the demon could freely copy every quantum particle it measured, it could retain flawless records while still resetting its memory, this avoiding the usual entropy cost. The theorem blocks this strategy by forbidding perfect duplication, ensuring that information can't be 'multiplied' without limit. Similarly, the principle of unitarity implies that a system will always evolve in a way that preserves overall probabilities. As a result, quantum phenomena can't selectively amplify certain outcomes while discarding others. For the demon, this means it can't secretly limit the range of possible states the system can occupy into a smaller set where the system has lower entropy, because unitarity guarantees that the full spread of possibilities is preserved across time.
All these rules together prevent the demon from multiplying or rearranging quantum states in a way that would allow it to beat the second law.
Then again, these 'blocks' that prevent Maxwell’s demon from breaking the second law of thermodynamics in the quantum realm raise a puzzle of their own: is the second law of thermodynamics guaranteed no matter how we interpret quantum mechanics? 'Interpreting quantum mechanics' means to interpret what the rules of quantum mechanics say about reality, a topic I covered at length in a recent post. Some interpretations say that when we measure a quantum system, its wavefunction "collapses" to a definite outcome. Others say collapse never happens and that measurement is just entangled with the environment, a process called decoherence. The Maxwell's demon thought experiment thus forces the question: is the second law of thermodynamics safe in a particular interpretation of quantum mechanics or in all interpretations?

Landauer's idea, that erasing information always carries a cost, also applies to quantum information. Even if Maxwell's demon used qubits instead of bits, it won't be able to escape the fact that to reuse its memory, it must erase the record, which will generate heat. But then the question becomes more subtle in quantum systems because qubits can be entangled with each other, and their delicate coherence — the special quantum link between quantum states — can be lost when information is processed. This means scientists need to carefully separate two different ideas of entropy: one based on what we as observers don't know (our ignorance) and another based on what the quantum system itself has physically lost (by losing coherence).
The lesson is that the second law of thermodynamics doesn't just guard the flow of energy. In the quantum realm it also governs the flow of information. Entropy increases not only because we lose track of details but also because the very act of erasing and resetting information, whether classical or quantum, forces a cost that no demon can avoid.
Then again, some philosophers and physicists have resisted the move to information altogether, arguing that ordinary statistical mechanics suffices to resolve the paradox. They've argued that any device designed to exploit fluctuations will be subject to its own fluctuations, and thus in aggregate no violation will have occurred. In this view, the second law is self-sufficient and doesn't need the language of information, memory or knowledge to justify itself. This line of thought is attractive to those wary of anthropomorphising physics even if it also risks trivialising the demon. After all, the demon was designed to expose the gap between microscopic reversibility and macroscopic irreversibility, and simply declaring that "the averages work out" seems to bypass the conceptual tension.
Thus, the philosophical significance of Maxwell's demon is that it forces us to clarify the nature of entropy and the second law. Is entropy tied to our knowledge/ignorance of microstates, or is it ontic, tied to the irreversibility of information processing and computation? If Landauer is right, handling information and conserving energy are 'equally' fundamental physical concepts. If the statistical purists are right, on the other hand, then information adds nothing to the physics and the demon was never a serious challenge. Quantum theory can further stir both pots by suggesting that entropy is closely linked to the act of measurement, of quantum entanglement, and how quantum systems 'collapse' to classical ones by the process of decoherence. The demon debate therefore tests whether information is a physically primitive entity or a knowledge-based tool. Either way, however, Maxwell's demon endures as a parable.
Ultimately, what makes Maxwell's demon a gift that keeps giving is that it works on several levels. On the surface it's a riddle about sorting molecules between two chambers. Dig a little deeper and it becomes a probe into the meaning of entropy. If you dig even further, it seems to be a bridge between matter and information. As the Schrödinger's cat thought experiment dramatised the oddness of quantum superposition, Maxwell's demon dramatised the subtleties of thermodynamics by invoking a fantastical entity. And while Schrödinger's cat forces us to ask what it means for a macroscopic system to be in two states at once, Maxwell's demon forces us to ask what it means to know something about a system and whether that knowledge can be used without consequence.



